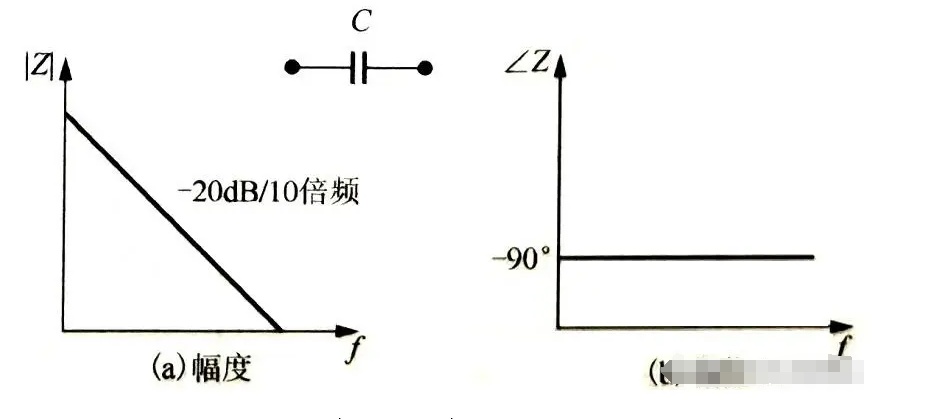
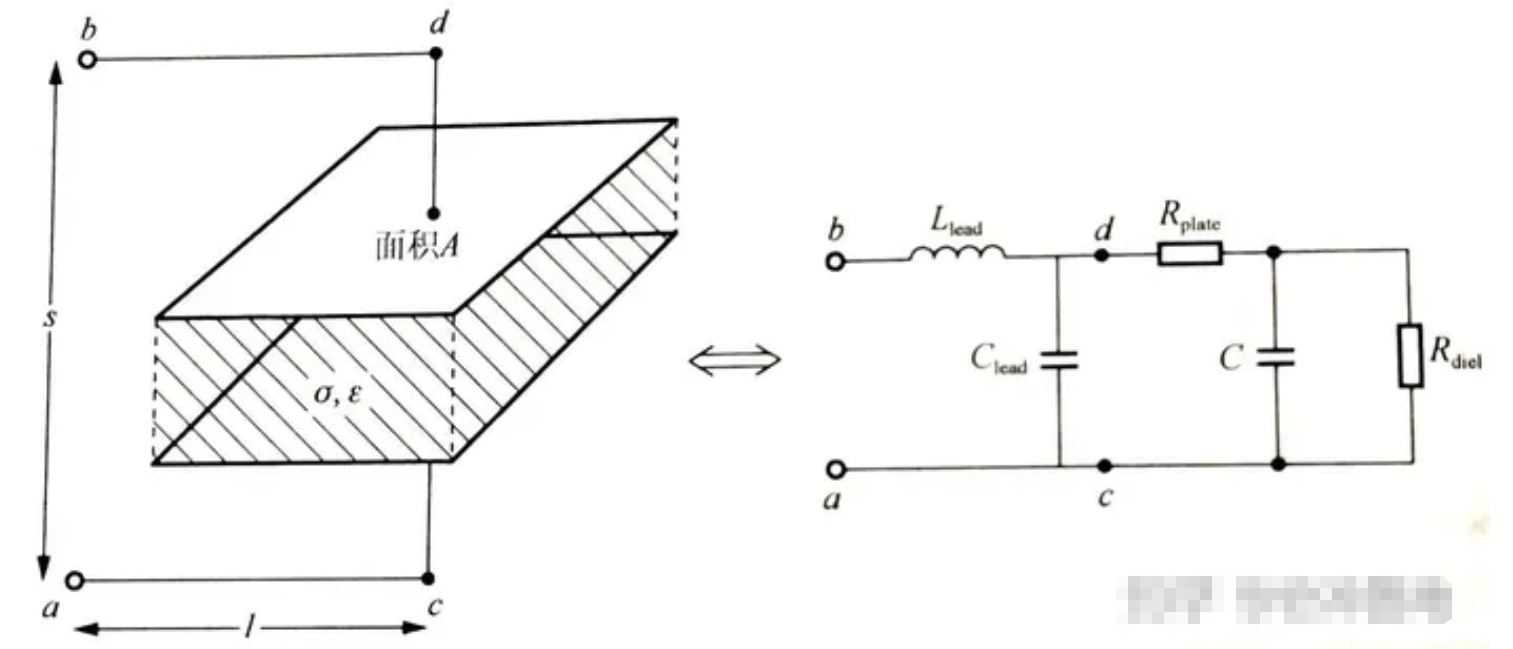
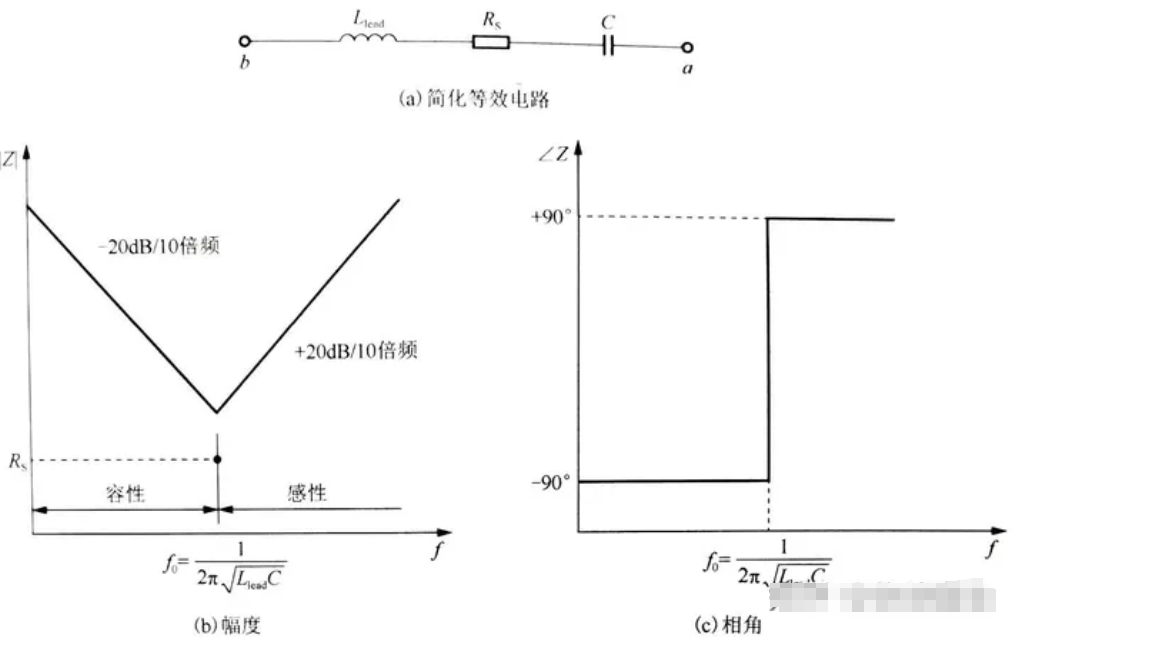
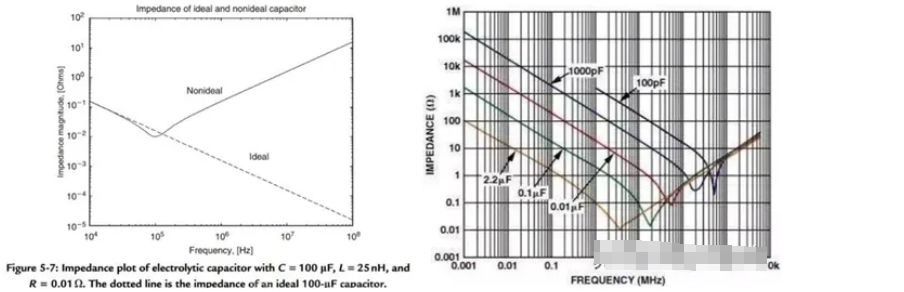
电容是“隔直通交”,就是对直流电有隔断作用,就是直流不能通过,而交流电可以通过,而且随着电容值的增大或者交流电的增大,电容对交流电的阻碍作用越小,这种阻碍作用可以理解为“电阻”,但是不等同于电阻,这是一种电抗,电抗和电阻单位一样,合称“阻抗”。 上。虽然,电阻、电容和电感对电路的影响完全不一样。但是都可以用阻抗公式体现出其对电路的影响来。 理想电容器的阻抗公式为:Z(jω) = 1/jωC = -j/ωC。其中,ω:信号角频率 (相位是-90°)。 我们知道电容的阻抗是虚数,那又表示了啥意思呢?它表达的是电容是对电磁能量 的“虚消耗”,即:不会消耗电磁能,只能存储或释放能量的动作。 一个理想电容器的频响特性图如下图所示,这其实就是电容对电路的影响: 1. 电容器阻抗的幅度| Z(jω)| = 1/ωc,其随频率线性减小,斜率为-20dB/10倍频(对数坐标 ); 2. 电容器的相角 在所有频率上都是-90°,Zc = Uc/Ic,所以它表示的是电压相对于电流的相位关系。 当然,我们知道电容器并非只是理想的电容特性,而是由电容、寄生电阻 。 但究其本质,电容器都可以看作由电介质隔开的一堆平行板,如下图所示; 1. 电介质中的损耗(极化和电阻性损耗)用并联电阻Rdiel 表示; ——这个电阻值非常大,在电容器中表现为漏电流 ,可以在电容器模型中忽略。 2. 平行板上的寄生电阻用Rplate表示; ——平行板金属材料的寄生电阻,非常小,对于小型陶瓷电容器来说,其值可以忽略;所以我们在陶瓷电容器 的spec上,通常看不到ESR这个参数。 3. 电容器引线上具有一定的寄生电感和电容,分别用:Llead和Clead表示; ——这些寄生电感和电容的大小取决于引线的结构,Clead一般比理想电容C要小得多,因此可以忽略。 4. 因此电容器的等效电路由C、Llead和Rplate的串联构成,其中Rplate称为等效串接电阻 或ESR,因此Rplate也就是Rs(ESR或Rs并非一直不变,而是随频率变化的,下面会详细介绍)。 如下图所示,可以得到电容器等效电路 模型的阻抗: Z(jω) = 1/jωC + Rs + jωL = (1+jωC*Rs-ω²C*L)/ jωC。 从该公式我们可以得到1个极点(分母为0的点:ω=0),2个零点(分子为0的点,忽略电阻的影响,零点 为:1/(2π√LC),电容器随频率增加的过程如下所示: 1. 在该模型中,直流时电路表现为开路; ——电感Lead 为短路,电容C为开路,所以它们串联后表现为开路状态。 2. 随着频率升高,容抗 (相角为接近-90°); 3. 直到频率增加到f0= 1/2π* Llead∗C 时电容的容抗与电感的感抗相等(阻抗值 为Rs(ESR);此时电容器的电路模型表现为阻性(相角为0°); ——f0称为自谐振频率点 。 4. 频率继续更加,此时感抗在电容电路 模型中占据主要作用,阻抗幅值随着频率的升高以+20dB/10倍频的速率增加;电容器的电容模型表现为感性(相角为接近+90°)。 ——我们如何去判断一个电路是容性、阻性还是感性,主要取决于电路中电压对于电流的相位关系,即阻抗相角:如果相角是0°,那么就是阻性的,如果相角<0°,那么就是容性的(-90°是纯电容),如果相角>0°则是感性的(90°是纯电感);相角体现了容性、阻性和感性之间占阻抗的比例关系。大家需要仔细品一品~ 对于很多应用来说,举个栗子:电源滤波需要考虑的是电容器的低阻抗来旁路噪声电流,那么最优频点必然是在电容器的自谐振频率点f0附近;但是电容器在不同阶段呈现了不同的特性:容性、阻性、感性,电流噪声频率比电容器的谐振点f0高行不行?或则说,电容器是否只能滤除自谐振频率f0以下的噪声呢? ——个人认为电容器呈现的是容性或则感性对滤波没有影响,即噪声频率可以高于f0也可以有良好的滤波;对于常用的器件电源滤波/去耦应用来说,我们需要的电容器是在该频率下对电源电流波动(噪声)的响应速度,即此时电容器的阻抗大小,而不是该阻抗的属性。 如下右图为相同材料、封装,不同容值电容器的二阶阻抗-频率特性图,我们定性分析如下: 1. 电容器容值的越小,低频段阻抗越大; ——根据电容器阻抗计算公式:Z = RE + jω *(Llead- 1/ω²C) ≈1/jωC,在相同信号频率下(ω相等),C越大阻抗越小(在低频段电容特性占主导作用)。 2. 电容器容值的越小,自谐振频率越大; ——自谐振频率点f0
= 1/(2π* Llead∗C
),假设同材料、封装的电容器Llead值相同:那么C越大,自谐振频率点f0就越小;而且C与f0的关系可以通过公式计算,例如C增大10倍(如上图:0.1uF和0.01uF),那么自谐振频率点f0就相差
10 = 3.16倍。 3. 不同容值的电容器,自谐振频点右侧(高频段)曲线重叠; ——如上分析,自谐振频率点后,电容器呈现电感特性:Z = RE + jω *(Llead -1/ω²C)≈jωLlead,其阻抗曲线斜率 取决于寄生电感Llead的大小,而相同材料、封装的电容器寄生电感值非常接近,而呈现在电容器阻抗曲线图中,就是自谐振频率点右侧的阻抗曲线相同。 4. 电容器容值的越小,Rs(ESR)呈上升趋势; ——电容器的ESR取决于电容器本身的材料、结构及封装,也同电容的工作频率有关。 寄生电阻和寄生电感与电容器本身的器件结构、封装、尺寸等影响很大,为减小寄生电阻、电感,最好使用小封装、贴片的电容器。不同的电容器有不同的阻抗-频率特性曲线,在实际应用中,我们需要根据不同的硬件设计应用,选择不同容值、材料、封装的电容器,达到最合适的效果
电容对电路的影响以及如何影响,就体现在它的阻抗公式